"Sieve of Eratosthenes" in Go

I stumbled upon this talk about the origins of Go, and in the talk Steve Francia mentioned the "Prime Sieve" algorithm (at about 26:35). I haven't heard about the algorithm, so I jumped to Google, even before hearing his explanation.

Turns out it's an ancient algorithm also called "Sieve of Eratosthenes", by the mathematician who created it. It is an efficent algorithm for finding all primes below a certain number. It does so by going from the smallest prime number 2, and removing all the multiples of 2 in the given set. By definition if they are a multiple of any number except 1 and themselves they are not prime. After you filter out the numbers, you go to the next number not filtered out already, in this case 3, and filter out all the multiples of 3. 4 would be skipped because it was already filtered out by 2. The numbers that "survive" at the end are prime. It's nicely explained by this gif from Wikipedia:

I also saw some implementations that seemed pretty straightforward. You generate a set of numbers and filter them out in a loop.

Okay, I now understood the algo, let's get back to the video. At about 33:55 Steve showed the Go concurent implementation of this algorithm. It didn't look anything close to the algorithms I saw just a few minutes ago. His 3 minute explanation wasn't that deep, understandably, so I went back to Google.

I found the code on The Go Playground. You should open the code and inspect it to follow along. I've played around with goroutines and channels previously, but mostly in excerices. The trickiest bit was that ch = ch1. What was that for?

Also, all implementations I saw were "find all primes below n" but this one was "find n prime numbers" (or ∞).

As per usual I added a few fmt.Printfs to better understand what was going on. The results were:

Gen() sending 2 to ch
Gen() sending 3 to ch
>>>> main() loop received 2
2
ch = ch1
Filter(2) received 3
>>>> main() loop received 3
3
ch = ch1
Gen() sending 4 to chain
Gen() sending 5 to chain
Filter(2) received 4
Filter(2) killed 4
Filter(2) received 5
Filter(3) received 5
>>>> main() loop received 5
5
ch = ch1

The Filter(2) killed 4 came from:

if i%prime != 0 {
  out <- i // Send 'i' to 'out'.
} else {
  fmt.Printf("Filter(%d) killed %d\n", prime, i)
}

What helped me understand the entire implementation was:

Filter(2) received 4
Filter(2) killed 4
Filter(2) received 5
Filter(3) received 5
>>>> main() loop received 5
5
ch = ch1

So, it looks like in order to be marked as prime, newly generated numbers must pass a series of filters. Where do we get that series of filters?

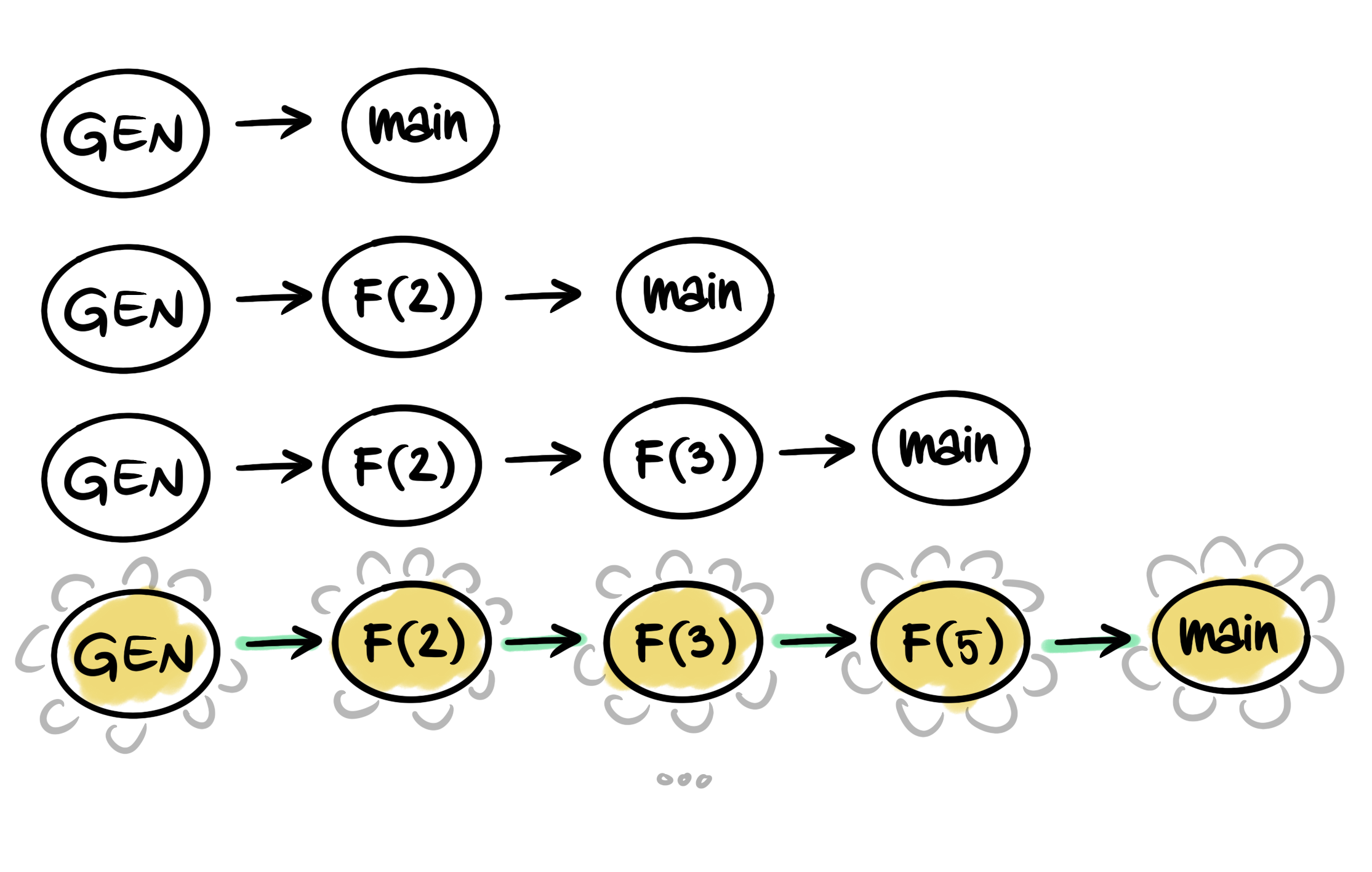
At the beggining there are no filters, so the main loop receives 2 from Generate, prints it to the console and creates a new goroutine Filter(ch, ch1, 2). Now comes the ch = ch1. Actually let's call the channels src (ch) and dst (ch1), it makes more sense. src = dst says "The input of the next Filter is the output of this one".

At about this point I understood the // Daisy-chain Filter processes comment.

Every newly generated number must pass all of the previously created daisy flower filters (goroutines). Here's the code with better output.

For example, all even numbers will be instantly filtered out by Filter(2) and never get further in the chain. Once a number passes all of the filters, it is considered prime and a new filter with that number is added to the chain. This is so elegant.

I hope you found this useful. Let me know on twitter how you liked it.

Bonus

What if we add time.Sleep(1 * time.Second) after the loop, and only leave the comments from Generate? The following is printed:

29 // the 10th prime we asked for
Gen() sent 30 to chain
Gen() sent 31 to chain
...
Gen() sent 67 to chain
Gen() sent 68 to chain

Even if we sleep for 5 seconds the Generate stops at 68. Why 68? Take a look at the code and try to figure it out for yourself.

[some time passes]

Because channels we use to connect the filters aren't buffered, a Filter() blocks if it cannot send a number further up the chain.

From 30 to 68, if you manually check, there are 9 primes! This is what the chain ends up looking like:

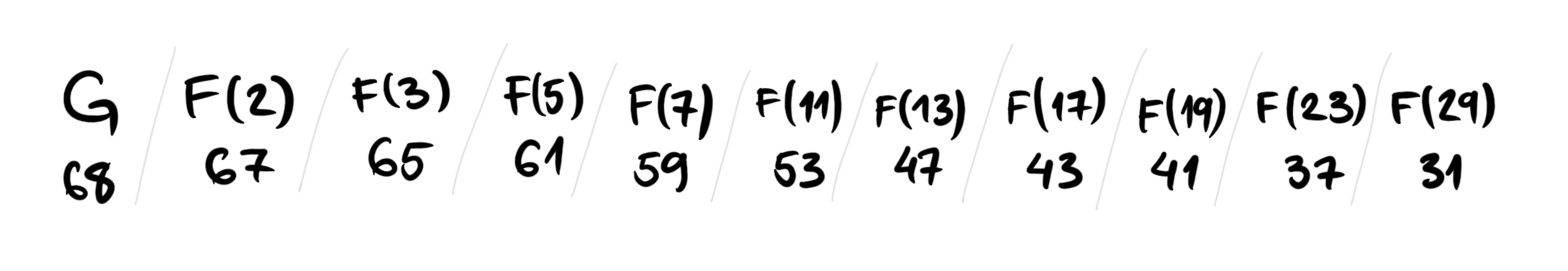
65 actually isn't prime but it will only be filtered out by Filter(5).